FallbrookAstro 2024-08-29 18:21
Starship and Superheavy are the next generation of spaceflight. Fly them here with real physics and real numbers to check out their power!
Game includes:
-Starship and Superheavy booster
-Hotstaging
-Wrapping world (WIP)
-Lack of proper physics
-ReadMe in the source code
Have fun!
nathanielbabiak 2024-08-30 01:08 (Edited)
There's a decent amount of math here - what source did you use for determining orbital parameters? (Ap and Pe?)
FallbrookAstro 2024-08-30 07:33
nathanielbabiak i used basic kinematics to start, but because the world is simulated as an x,y parametric plane, it’s hard to make things go to orbit, so i played around with the formulas but still haven’t found any that work
SP4CEBAR 2024-08-30 12:16 (Edited)
@FallbrookAstro This is awesome!
Here's a trick that may make your simulation easier:
You can define a polar (R, A) plane with the origin at the earth's center. Since the planet is pretty big (r is at least 6,371 kilometers), any terrain loader can treat "R" as "Y" and the circumference "R*A" (A is in radians) as "x", while the physics engine can use the polar values.
Whenever your SOI changes, you can set the new body as your center.
nathanielbabiak 2024-08-30 14:08 (Edited)
yeah I found a number of sources for the orbital mechanics, but none that use so few intermediate equations to develop apoapsis and periapsis from newtonian physics.
honestly, I was kind of hoping you found a better source that would provide a bit of a shortcut…
hey, if you're ever interested in checking out my favorite source, it's this one
SP4CEBAR 2024-08-30 15:59 (Edited)
By "Newtonian physics" are you referring to a game loop that recursively adds the acceleration to the velocity and the velocity to the position? If so then Equation 4.45 from the source can be used. The equation gives the velocity for a given radius and ellipse "a" parameter.
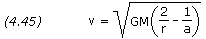
The equation can be rewritten to calculate the "a" parameter of the ellipse, this brings us one step closer to figuring out the ellipse (we just need the eccentricity).
There might still be something useful in my last study
FallbrookAstro 2024-08-30 16:16
eccentricity was my biggest issue, there was almost no way to derive it from the physics i implemented. i may start from scratch again and try it in polar
SP4CEBAR 2024-08-30 18:42 (Edited)
If you can't derive it, try the Newton–Raphson method
SP4CEBAR 2024-08-30 18:56
I think the problem we are trying to solve is solved in problem 4.8
FallbrookAstro 2024-09-03 18:19
SP4CEBAR that looks like exactly the solution i need! will work on it and report back. thank you!
SP4CEBAR 2024-09-04 09:58
Good luck!
